Fluorocarbon Etching
#include <psFluorocarbonEtching.hpp>
Our model assumes that, in any complex plasma etch process, there are four fundamental types of particles: neutral, etchant, depositing polymer particles and ions. Due to the long etch times, compared to surface reaction time scales, we can safely assume that each of these substances’ concentrations will reach a steady state on the surface. Therefore, the surface coverages of all involved particle types $\phi_x$, where $x$ represents etchant (e), polymer (p), etchant on polymer (ep), and ions (i), are expressed by the following equations: \begin{equation} \frac{d \phi_e}{dt}=J_{e} S_{e}\left(1-\phi_{e}-\phi_{p}\right)-k_{i e} J_{i} Y_{ie} \phi_{e}-k_{e v} J_{e v} \phi_{e} \approx 0; \end{equation} \begin{equation} \frac{d \phi_{p}}{d t}=J_{p} S_{p}-J_{i} Y_{p} \phi_{p} \phi_{p e} \approx 0; \end{equation} \begin{equation} \frac{d \phi_{p e}}{d t}=J_{e} S_{p e}\left(1-\phi_{p e}\right)-J_{i} Y_{p} \phi_{p e} \approx 0. \end{equation} Here, $J_x$ and $S_x$ represent the different particle fluxes and sticking probabilities, respectively. $Y_{ie}$ is the ion-enhanced etching yield for etchant particles, $Y_p$ is the ion-enhanced etching yield on polymer, $Y_{sp}$ gives the physical ion sputtering yield, and $k_{ie}$ and $k_{ev}$ are the stoichiometric factors for ion-enhanced etching and evaporation, respectively, which are determined by the chemical etching reaction. By solving these steady state equations for the coverages, one can determine etch or deposition rates on the surface. If deposition of polymer dominates, the surface normal velocity is positive and is given by \begin{equation} v=\frac{1}{\rho_{p}}\left(J_{p} S_{p}-Y_{p} J_{i} \phi_{p e}\right), \end{equation} where $\rho_p$ is the atomic polymer density. The first term $J_{p} S_{p}$ gives the rate of polymer particles reaching and adsorbing on the surface, while the second term $Y_{p} J_{i} \phi_{p e}$ describes the removal of polymer by ion-enhanced etching. Together, these terms describe the deposition of polymer material on the surface, which acts as passivation layer for the chemical etching process. If, on the other hand, etching of the substrate dominates, the negative surface velocity of the substrate is given by \begin{equation} v=\frac{1}{\rho_{m}}\left[J_{e v} \phi_{e}+J_{i} Y_{ie} \phi_{e}+J_{i} Y_{sp}\left(1-\phi_{e}\right)\right], \end{equation} where $\rho_m$ is the atomic density of the etched material and depends on which layer in the stack is being etched. Each term accounts for a different type of surface reaction. The first term, $J_{e v} \phi_{e}$, describes the chemical etching process, where etchants bind chemically with the substrate to form volatile etch products which dissolve thermally from the surface. Thus, the evaporation flux $J_{ev}$ is a parameter proportional to the etchant flux $J_e$ and depends on the chemical gas and surface composition and temperature of the etching plasma. It is given by \begin{equation} J_{ev} = K e^{-E_a/k_B T}J_e, \end{equation} where $K$ is a process parameter describing the volatility of the chemical etching process, $E_a$ is the activation energy for thermal etching, $k_B$ is the Boltzmann constant, and $T$ is the temperature. The second term, $J_{i} Y_{ie} \phi_{e}$, describes the contribution of ion-enhanced etching. In this surface reaction, volatile etch products which do not dissolve from the surface thermally, absorb energy from impinging ions and consequently dissolve from the surface. Finally, the last term, $J_{i} Y_{sp}\left(1-\phi_{e}\right)$, describes physical sputtering of the substrate by highly energetic ions. Since both chemical and ion-enhanced etching involve etchants, they are proportional to the etchant coverage $\phi_e$, while physical ion sputtering takes place directly on the substrate and is thus proportional to the fraction of the surface not covered by the etchant.
Ions
Each ion is endowed with an initial energy and direction upon creation on the source plane. The assignment of initial energies is governed by a normal distribution, characterized by a mean energy value and an energy sigma, thus allowing for stochastic variations in the initial energy states of the ions. The distribution of initial ion directions is given by a power cosine source distribution, which is defined by the exponent of the power cosine distribution.
Upon impact with the surface, an energy- and angle-dependent yield is computed, which contributes to the specific surface point’s rate. The yield is expressed as: \begin{equation} Y(E,\theta) = A\left(\sqrt{E} - \sqrt{E_{th}}\right)f(\theta), \end{equation} where $E$ denotes the particle energy and $\theta$ its incident angle. Here, $A$ represents a yield coefficient, and $E_{\text{th}}$ denotes the material’s threshold energy for physical sputtering. The function $f(\theta)$, which characterizes the angle-dependence of the yield. For sputtering, the function is given by: \begin{equation} f(\theta) = (1 + B_{sp}(1-\cos^2(\theta)))\cos(\theta), \end{equation} while for ion-enhanced etching, the function is given by: \begin{equation} f(\theta) = \cos(\theta). \end{equation}
The ions can also reflect from the surface. Their energy loss during reflection is described by the model proposed by Belen et al [^1]. The current ray energy is multiplied by a factor $E_\textrm{ref}$ ($0 \leq E_\textrm{ref} \leq 1$) which depends on the incoming angle $\theta$ in the following way: \begin{equation} E_{\textrm{ref}}= 1-(1-A)\frac{\frac{\pi}{2}-\theta}{\frac{\pi}{2}-\theta_\textrm{inflect}} \quad \text{ if } \theta \geqslant \theta_\textrm{inflect} \end{equation} \begin{equation} E_{\textrm{ref}}=\mathrm{A}\left(\frac{\theta}{\theta_\textrm{inflect}}\right)^{n_l} \quad \text{ if } \theta<\theta_\textrm{inflect}, \end{equation} where $A = (1 + n(\frac{\pi}{2 \theta_\textrm{inflect}} - 1))^{-1}$.
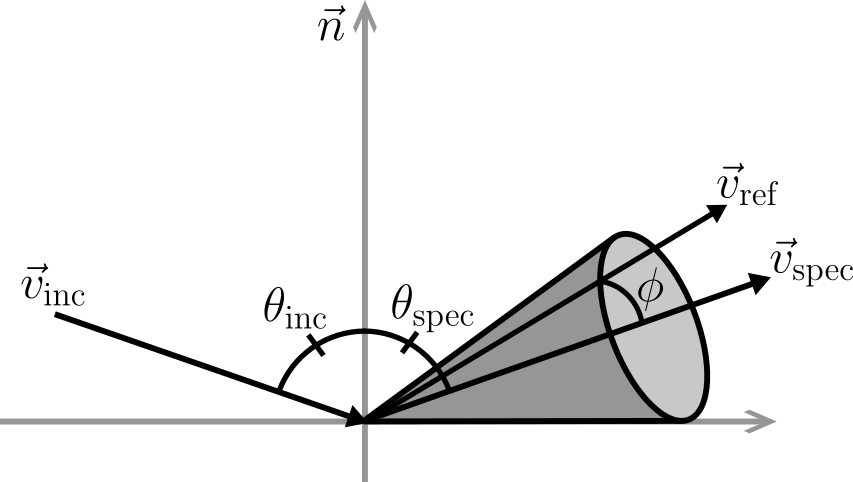
Ions striking the surface at an angle denoted by $\theta$ relative to the surface normal undergo reflection, where the angular dispersion is characterized by a cosine function centered around the direction of specular reflection defined by $\theta_\textrm{spec}$. This reflection process distinguishes between ions approaching the surface at glancing angles, which undergo nearly perfect specular reflection, and those striking the surface perpendicularly, which undergo nearly diffuse reflection.
\begin{equation} \mathrm{P}(\phi) \propto \cos \left(\frac{\pi}{2} \frac{\phi}{\frac{\pi}{2}-\theta_\textrm{spec}}\right) \quad \text{ if } \theta_\textrm{inc} \leqslant \theta_\textrm{min} \end{equation}
\begin{equation} \mathrm{P}(\phi) \propto \cos \left(\frac{\pi}{2} \frac{\phi}{\frac{\pi}{2}-\theta_\textrm{min}}\right) \quad \text{ if } \theta_{\textrm{inc}}>\theta_{\textrm{min}} \end{equation}
The ray’s reflected direction is randomly chosen from a cone around the specular direction. The opening angle of this cone is given by the incidence angle $\theta$.
Implementation
The fluorocarbon etching process is implemented in the psFluorocarbonEtching class. To customize the parameters of the process, it is advised to create a new instance of the class and set the desired parameters in the parameter struct. The following example demonstrates how to create a new instance of the class and set the parameters of the process.
C++
// namespace viennaps
...
auto model = SmartPointer<FluorocarbonEtching<NumericType, D>>::New();
auto ¶meters = model->getParameters();
parameters.ionFlux = 10.;
parameters.Mask.rho = 500.;
// this modifies a direct reference of the parameters
...
Python
...
model = vps.FluorocarbonEtching()
parameters = model.getParameters()
parameters.ionFlux = 10.
parameters.Mask.rho = 500.
# this modifies a direct reference of the parameters
...
The strcut holds the following parameters:
| Parameter | Description | Default Value |
|---|---|---|
ionFlux | Ion flux (1015 /cm² /s) | 56.0 |
etchantFlux | Etchant flux (1015 /cm² /s) | 500.0 |
polyFlux | Polymer flux (1015 /cm² /s) | 100.0 |
etchStopDepth | Depth at which etching stops | -inf |
temperature | Temperature (K) | 300.0 |
k_ie | Stoichiometric factor for ion enhanced etching | 2.0 |
k_ev | Stoichiometric factor for chemical etching | 2.0 |
beta_p | Polymer clean surface sticking probability | 0.26 |
beta_e | Etchant clean surface sticking probability | 0.9 |
beta_pe | Sticking probability for etchant on polymer | 0.6 |
delta_p | Amount of polymer need to cause deposition of the surface | 1.0 |
Mask.rho | Mask density (1022 atoms/cm³) | 500.0 |
Mask.beta_p | Polymer clean surface sticking probability on mask material | 0.01 |
Mask.beta_e | Etchant clean surface sticking probability on mask material | 0.1 |
Mask.A_sp | Mask sputtering coefficient | 0.0139 |
Mask.B_sp | Mask yield coefficient | 9.3 |
Mask.Eth_sp | Mask sputtering threshold energy (eV) | 20.0 |
SiO2.rho | SiO2 density (1022 atoms/cm³) | 2.2 |
SiO2.Eth_sp | SiO2 sputtering threshold energy (eV) | 18.0 |
SiO2.Eth_ie | SiO2 on enhanced etching threshold energy (eV) | 4.0 |
SiO2.A_sp | SiO2 sputtering coefficient | 0.0139 |
SiO2.B_sp | SiO2 yield coefficient | 9.3 |
SiO2.A_ie | SiO2 ion enhanced etching coefficient | 0.0361 |
SiO2.K | SiO2 volatility parameter in evaporation flux | 0.002789491704544977 |
SiO2.E_a | SiO2 activation energy (eV) | 0.168 |
Polymer.rho | Polymer density (1022 atoms/cm³) | 2.0 |
Polymer.Eth_ie | Polymer ion enhanced etching threshold energy (eV) | 4.0 |
Polymer.A_ie | Polymer ion enhanced etching coefficient | 0.1444 |
Si3N4.rho | Si3N4 density (1022 atoms/cm³) | 2.3 |
Si3N4.Eth_sp | Si3N4 sputtering threshold energy (eV) | 18.0 |
Si3N4.Eth_ie | Si3N4 ion enhanced etching threshold energy (eV) | 4.0 |
Si3N4.A_sp | Si3N4 sputtering coefficient | 0.0139 |
Si3N4.B_sp | Si3N4 yield coefficient | 9.3 |
Si3N4.A_ie | Si3N4 ion enhanced etching coefficient | 0.0361 |
Si3N4.K | Si3N4 volatility parameter in evaporation flux | 0.002789491704544977 |
Si3N4.E_a | Si3N4 activation energy (eV) | 0.168 |
Si.rho | Si density (1022 atoms/cm³) | 5.02 |
Si.Eth_sp | Si sputtering threshold energy (eV) | 20.0 |
Si.Eth_ie | Si ion enhanced etching threshold energy (eV) | 4.0 |
Si.A_sp | Si sputtering coefficient | 0.0337 |
Si.B_sp | Si yield coefficient | 9.3 |
Si.A_ie | Si ion enhanced etching coefficient | 0.0361 |
Si.K | Si volatility parameter in evaporation flux | 0.029997010728956663 |
Si.E_a | Si activation energy (eV) | 0.108 |
Ions.meanEnergy | Mean ion energy (eV) | 100.0 |
Ions.sigmaEnergy | Standard deviation of ion energy (eV) | 10.0 |
Ions.exponent | Exponent of power cosine source distribution of initial ion directions | 500.0 |
Ions.inflectAngle | Inflection angle | 1.55334303 |
Ions.n_l | Exponent of reflection power | 10.0 |
Ions.minAngle | Minimum cone angle for ion reflection | 1.3962634 |