Multi Particle Process
#include <psMultiParticleProcess.hpp>
The multi particle process is a simple process model that simulates either etching or deposition, where an arbitrary number of particles can be specified. The particles can be neutral or ions, and the model can be used to simulate a wide range of processes. The rate equation for combining the fluxes of the particles has to be provided by the user.
Neutral Particles
Neutral particles are defined by their sticking probability, which is the probability that a neutral particle will stick to the surface upon impact. The sticking probability is a value between 0 and 1. The sticking probability defines the reflection behavior of the neutral particles. A sticking probability of 1 means that the neutral particle will always stick to the surface, while a sticking probability of 0 means that the neutral particle will always be reflected.
Ion Particles
Ion particles are defined by their source exponent, which is the exponent of the power cosine distribution for the initial directions of the ions. The source exponent defines the distribution of the initial directions of the ions. A source exponent of 1 means that the ions are emitted isotropically, while a source exponent of 1000 means that the ions are emitted mostly perpendicular to the surface.
The ion sticking function is defined by the parameters $\theta_{min}$ and $\theta_{max}$. The ion sticking function is a function of the incoming angle $\theta$ that defines the probability that an ion will stick to the surface upon impact. The ion sticking function is a linear function defined as:
\[S(\theta) = \begin{cases} 0 & \text{if } \theta < \theta_{min} \\ 1 & \text{if } \theta > \theta_{max} \\ \frac{\theta - \theta_{min}}{\theta_{max} - \theta_{min}} & \text{otherwise} \end{cases}\]Ions striking the surface at an angle denoted by $\theta$ relative to the surface normal undergo reflection, where the angular dispersion is characterized by a cosine function centered around the direction of specular reflection defined by $\theta_\textrm{spec}$. This reflection process distinguishes between ions approaching the surface at glancing angles, which undergo nearly perfect specular reflection, and those striking the surface perpendicularly, which undergo nearly diffuse reflection. The ray’s reflected direction is randomly chosen from a cone around the specular direction. The opening angle of this cone is given by the incidence angle $\theta$ or the minimum specified angle $\theta_{min}$.
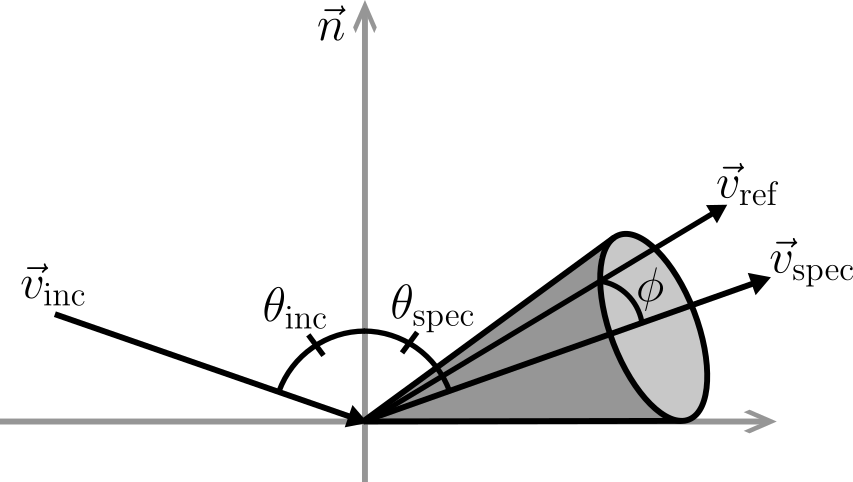
Optional Parameters:
Ion can be assigned an energy which can be used to calculate a surface yield. This feature can be activated by setting the mean energy > 0 and is deactivated by setting the mean energy = 0. The energy distribution of the ions is assumed to be Gaussian with a standard deviation of sigmaEnergy. The threshold energy is the energy below which the ion will not sputter the surface, and the energy dependent yield is defined as:
\[Y(E) = \begin{cases} 0 & \text{if } E < E_{\textrm{threshold}} \\ \sqrt{E} - \sqrt{E_{\textrm{threshold}}} & \text{if } E \geq E_{\textrm{threshold}} \end{cases}\]The inflection angle and n are parameters of the ion energy reduction function, which is used to calculate the energy after reflection. The ion energy reduction function is defined as:
\[E_{\textrm{ref}}= \begin{cases} 1-(1-A)\frac{\frac{\pi}{2}-\theta}{\frac{\pi}{2}-\theta_\textrm{inflect}} & \text{ if } \theta \geqslant \theta_\textrm{inflect} \\ \mathrm{A}\left(\frac{\theta}{\theta_\textrm{inflect}}\right)^{n_l} & \text{ if } \theta<\theta_\textrm{inflect}, \end{cases}\]where $A = (1 + n(\frac{\pi}{2 \theta_\textrm{inflect}} - 1))^{-1}$.
The angle-dependent sputtering yield is defined as:
\begin{equation} Y(\theta) = (1 + B_{sp}(1-\cos^2(\theta)))\cos(\theta). \end{equation}
Implementation
// default empty constructor
MultiParticleProcess()
void addNeutralParticle(NumericType stickingProbability)
void addIonParticle(NumericType sourceExponent,
NumericType thetaRMin = 0.,
NumericType thetaRMax = 90.,
NumericType minAngle = 0.,
NumericType B_sp = -1.,
NumericType meanEnergy = 0.,
NumericType sigmaEnergy = 0.,
NumericType thresholdEnergy = 0.,
NumericType inflectAngle = 0.,
NumericType n = 1)
void setRateFunction(std::function<NumericType(std::vector<NumericType> &,
const Material &)> rateFunction)
| Parameter | Description | Default Value |
|---|---|---|
stickingProbability | Sticking probability of the neutral particle | - |
sourceExponent | Exponent of the power cosine distribution for the initial directions of ions | - |
thetaRMin | $\theta_{min}$ in the ion sticking function | 0.0 |
thetaRMax | $\theta_{max}$ in the ion sticking function | 90.0 |
minAngle | Minimum angle for the ion reflection | 0.0 |
B_sp | Sputtering yield parameter | -1.0 |
meanEnergy | Mean initial energy of the ions | 0.0 |
sigmaEnergy | Standard deviation of the initial energy of the ions | 0.0 |
thresholdEnergy | Threshold energy for ion sputtering | 0.0 |
inflectAngle | Inflection angle of the ion energy reduction function | 0.0 |
n | Exponent of the ion energy reduction function | 1.0 |
Example usage:
C++
...
auto model = SmartPointer<MultiParticleProcess<NumericType, D>>::New();
model->addNeutralParticle(0.1);
model->addIonParticle(1000.);
// for material specific rates
auto rateFunction = [](std::vector<NumericType> &fluxes, const Material &material) {
// fluxes contains the neutral flux at first index and ion flux at second index
return material == Material::Si ? -(fluxes[0] + fluxes[1]) : 0.;
};
model->setRateFunction(rateFunction);
...
Python
...
model = vps.MultiParticleProcess()
model.addNeutralParticle(0.1)
model.addIonParticle(1000.)
# for material specific rates
def rateFunction(fluxes, material):
if material == vps.Material.Si:
# fluxes contains the neutral flux at first index and ion flux at second index
return -sum(fluxes)
else:
return 0.
model.setRateFunction(rateFunction)
...